Chapter
2
This chapter provides a summary of the principles of scientific inquiry. The purpose is to explain terminology, and introduce concepts, which are explained more completely in later chapters. Much of the content has been based on explanations and examples given by Wilson (1).
Although most of us have heard, at some time in our careers, that research must be carried out according to “the scientific method”, there is no single, scientific method. The term is usually used to mean a systematic approach to solving a problem in science. Three types of investigation, or method, can be recognized:
· The Observational Method
· The Experimental (and quasi-experimental) Methods, and
· The Survey Method.
The observational method is most common in the natural sciences, especially in fields such as biology, geology and environmental science. It involves recording observations according to a plan, which prescribes what information to collect, where it should be sought, and how it should be recorded. In the observational method, the researcher does not control any of the variables. In fact, it is important that the research be carried out in such a manner that the investigations do not change the behaviour of what is being observed. Errors introduced as a result of observing a phenomenon are known as systematic errors because they apply to all observations. Once a valid statistical sample (see Chapter Four) of observations has been recorded, the researcher analyzes and interprets the data, and develops a theory or hypothesis, which explains the observations.
The experimental method begins with a hypothesis. An experiment is designed to test the hypothesis by observing the response of one variable to changes in a limited number of other variables under controlled conditions. The data are analysed to determine whether a relationship exists which either confirms or refutes the hypothesis. The experimental method is frequently used in investigations in the physical sciences and engineering. The essential steps in the observational and experimental methods are illustrated in Figure 2. In both methods, establishing relationships may include the development of models to explain the relationships being postulated. Occasionally, the observational method may lead to a hypothesis, which is subsequently tested by the experimental method.
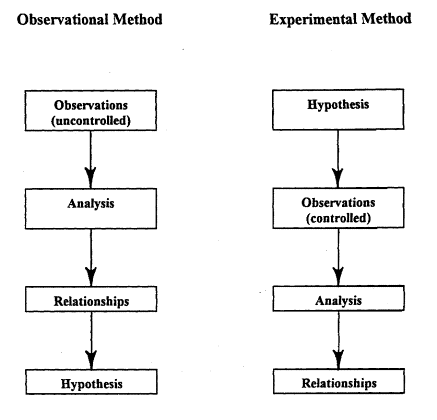
Figure 2: Steps in the Observational and Experimental Scientific Methods
Surveys and are a means of obtaining information not generally available under other circumstances, and are often used in the social sciences. The most common examples in transportation involve driver behaviour. As with the observational method, it is important that the act of collecting the data not change the behaviour being recorded, but, unlike observations, there is usually some interaction between the researcher and the subjects being studied. Three types of surveys can be recognized: historic, current and prospective. Historic surveys collect data on how things were in the past with the intent of explaining certain phenomena. A current survey examines how things are now, such as attitudes to new traffic signs. A prospective survey selects a group of people today and examines the same people at future times to investigate changes. Prospective surveys are often used in medical research, for example, to examine the incidence of cancer or heart disease in a segment of the population.
The terms “theory” and “hypothesis” are sometimes used interchangeably, but there is an important distinction between the terms. A hypothesis is an idea put forward to explain certain facts, and which can be tested. A theory is broader in scope and constitutes a conceptual framework that seeks to explain the connection of events and enables other relationships to be predicted. From a theory, it should be possible to derive testable hypotheses, which, if supported by the data, enhance the validity of the theory. Usually, many related hypotheses have to be tested and verified, before one has confidence in the validity of a theory. The connection between the data and the hypothesis is much stronger than between the data and the theory, which is conceptual and results from an intellectual process.
A hypothesis is a trial idea concerning the nature and connection of events. Hypotheses can be stated in a number of different forms (6). The declarative form states a relationship between the variables that the researcher expects will emerge. For example, “There will be a significant difference in the 3-day strength of concrete made with Type III (high early strength) cement compared with concrete made with Type I (ordinary Portland) cement”. Another form is the null hypothesis, or the hypothesis to be nullified. A special case of the null hypothesis is the nil hypothesis—which states that no relationship exists between the variables concerned. For example, in nil form, the hypothesis becomes, “There will be no significant difference in the 3-day strengths of concretes made with Type I and Type III cements”. The nil hypothesis does not necessarily reflect the researcher’s expectations, but is used because it is better suited to statistical techniques, many of which are designed to measure the likelihood that a difference found is truly greater than zero. In other words, the nil hypothesis, in the form usually used in science and engineering, states that no difference exists, and the statistical tools test this hypothesis by determining the probability that whatever difference is recorded by the experimental data is a true difference that will be present in the population from which the samples have been drawn. It is important to note that the form of the test hypothesis can favor, disadvantage, or be neutral to the challenging or alternative hypothesis. The researcher should be aware of the implications of the form of the nil and alternative hypotheses, and the practical implications of these choices. For instance, if the cost of conversion (from a standard method, procedure, etc.) is high, then the hypothesis might be chosen to put the challenger at a disadvantage, thereby helping to insure that change will occur only if the challenger is truly better.
The null and nil hypotheses can sometimes be confusing, especially to students, because it is the exact opposite of one’s expectations. One way to overcome this problem is to use a research hypothesis that reflects one’s expectations, and a statistical hypothesis, which is usually the null hypothesis, and which allows a more precise statistical evaluation of the research hypothesis.
Hypotheses may also be stated in question form. For example, “Is there a significant difference in the 3-day strength of concrete made with Type I or Type III cement?” This form is often the easiest for the inexperienced research worker because it states specifically the question the researcher is attempting to answer.
In cases where the researchers have good reason to expect a difference to occur in a specific direction, the hypothesis may be stated (using the same example) as “The 3-day strength of concrete made with Type III cement will be significantly greater than the 3-day strength of concrete made with Type I cement”, referred to as the null hypothesis. This type of hypothesis should only be used where there is little or no possibility that the data will yield a difference in the opposite direction. These two forms of declarative hypothesis call for a different statistical treatment. If the difference could occur in either direction, a two-tailed test is required, whereas a one-tailed test presumes that, if a difference occurs, it could occur in only one direction.
In the experimental method we begin by postulating a relationship, and then designing an experiment that will either support or refute our hypothesis. For example, if our hypothesis states that air and water are necessary to cause the corrosion of steel, we can construct the following simple experiment. We place nails in three test tubes, one containing de-aerated water, one with oxygenated water, and the other containing dry air. If the nails in oxygenated water begin to rust, but those in the other two test tubes do not, we can conclude that our hypothesis is valid. If any other combination of events occurs, we have shown our hypothesis to be incorrect.
In the observational method, the hypothesis is constructed to explain the observations. A simple one may be a generalization of the observations. A more complex hypothesis may postulate a relationship between the events, and may even be used to predict other observations.
If two different hypotheses fit the observed facts, and if one is clearly simpler than the other, it is customary to accept the simpler hypothesis until further evidence causes its rejection. A simple example is instructive. Suppose that the following numbers are observed:
3, 6, 9, 12, 15
A reasonable hypothesis would be that the data follow the sequence 3n (n=1, 2, 3...) and that the succeeding numbers would be 18, 21. However, the original data can equally be explained by the formula:
3n + (n-1)(n-2)(n-3)(n-4)(n-5)
or n=1, 2, 3... This formula would predict the next two numbers in the series to be 138, 741, which are quite different from the first hypothesis. While the simpler explanation is preferred, the second hypothesis cannot be discounted. For this reason, few scientists would claim that any hypothesis, no matter how rigorously it has been tested, to be a statement of the absolute truth. It is more likely to be a good explanation within a finite range of circumstances, the boundaries of which are not well demarcated. As further studies are made, the boundaries are defined more specifically, or a new hypothesis, having a more general application developed. A good example of this is Newton’s Laws of Motion, which could not explain the behavior of atomic particles, and were modified by the laws of quantum mechanics. However, Newton’s laws continue to be valid within a range of conditions which have been defined by modern science and which Newton could not have known about.
If the hypothesis under consideration is a simple generalization, it may be sufficient to test it by looking for more examples, and seeing whether the generalization holds true. Under these circumstances, unfavorable examples may lead to a refinement of the hypothesis, or if the unfavorable examples outweigh the favorable ones, to its outright rejection. It may be possible to develop a new hypothesis that fits the new, and old, data equally well.
Successful prediction is usually considered stronger support for a hypothesis than a simple explanation of observations. This is because the hypothesis should not only fit the facts that led to its development, but it should also be compatible with other scientific observations. In some cases, particularly in fields such as particle physics and astronomy, direct verification of a hypothesis is not possible. In such cases, deductions from the hypothesis are tested. If the deductions can be verified, this generates considerable confidence in the validity of the original hypothesis. This process is known as testing the core assumptions of a hypothesis.
Despite the ephemeral nature of even the best hypotheses, the word law is used for those that have stood extensive tests. A scientific law does not exclude the possibility that someday, under some set of circumstances, there may be data that cause us to change the law, as in the case of Newton’s Laws. A law is merely a relationship that so far as is known is invariable under the stated conditions. The laws of science are forever changing, but the changes are usually evolutionary in character, and more often represent refinements, or extensions, of existing laws than wholesale change.
We are all observers in our waking hours, but there are characteristics of scientific observations that distinguish them from our everyday observations. One of the most important is that scientific observations should be recorded immediately in a notebook. Human memory is much too fallible to rely upon recording data at some convenient time after the event. The requirements for keeping a good notebook are discussed in Chapter Five. In discussing observations, we are referring not only to observations made with the naked eye, but also to data collected by, or with the aid of, instruments.
Observation involves selection and description. We cannot describe the entire universe, and it is necessary to limit the scope of the observations to what is expected to disclose the interrelationships we are investigating. For example, if we are investigating whether a relationship exists between exposure to deicing salts and the health of fruit trees, we must select the trees to be observed and characteristics of the trees that are most likely to be affected by salt. In this case, a viable study plan would involve the examination of a representative sample of trees at varying distances from the highway for evidence of dieback and bud damage, (in the winter months) or reduced fruit production and foliar necrosis (in the summer months). We would also measure the salt concentration at various locations in the orchard to establish the relationship between salt concentration and distance from the highway. It would be impractical to observe all the trees in the orchard, or to describe all the characteristics of each tree.
It is important to recognize that in selecting the observations to be recorded, we have a major influence over the success of the investigation. An unwise choice of items to observe could mean that we would never discover relationships that might exist. This also implies that we must have a hypothesis in mind before making observations. This is inevitable, because if it were not so, we could not select what we should observe, but also undesirable, because we may introduce bias and preconceived prejudices. This is a relatively common trap, even among established researchers. When initial data tends to confirm an expected result, especially one previously reported by the researcher, there is a tendency to overlook contradictory data and not seek an alternative explanation. We must be very conscious that we do not allow our bias to distort our observations. This is far less easy than it sounds, and the work plan must be devised to ensure that the “true” facts are recorded in the notebook. One approach is to repeat the work, using a different sample, or a different site. Better still, would be to arrange for the observations to be made and recorded by others. Where an investigation cannot be repeated easily, for example if it involves an expensive crash test, it is important to use multiple, independent observers, and also to record the phenomena for later study, as for example, by photography.
Descriptions can be lengthy, and yet imprecise. It is desirable for scientific observations to be quantitative, and to use numbers to summarize qualitative observations wherever possible, even though the scale might be somewhat arbitrary. In the example discussed previously, we might establish a five-point, or a ten-point, scale that describes the condition of the fruit buds. This has the advantages of simplifying the recording of the observations and also renders the data more amenable to analysis.
Much has been written on the philosophy of cause and effect, but we need be concerned here only with the concept and the practical implications. As noted in Chapter One, we must be very careful to distinguish between a casual relationship (or correlation) and a causative relationship. This can be illustrated by an absurd example. In any large city in North America, the number of live births correlates very strongly with the number of automobiles over a period of, say, the past 40 years. However, no one would suggest that more automobiles are directly responsible for improved infant mortality rates. More often, the presence or absence of a causative relationship is less obvious. Many researchers have suggested that an increase in the chloride ion content of concrete causes an increase in the rate of corrosion of embedded reinforcement. However, increased understanding of the mechanisms involved, supports a model that predicts that corrosion will begin once a threshold value of chloride ions is exceeded, and that additional chloride ions have little effect on the corrosion rate. It is true that there is a strong correlation between chloride ion content and corrosion rate, but the relationship is not one of cause and effect. Once corrosion has begun, the rate of corrosion and the chloride ion content will increase independently as a function of time, as long as the concrete continues to be exposed to salt.
Three conditions must be satisfied before a causative relationship can be established:
· consistency
· responsiveness, and
· a mechanism.
The consistency requirement means that the two correlated events occur as a pair and, if the first occurs, the second accompanies or follows it. Further, to satisfy the consistency requirement, the same sort of correlation (if not exactly the same result) must occur each time the test is run or the observation is made.
Responsiveness means that the change in the independent variable results in a change in the dependent variable (variables are discussed in more detail in Chapter Four). The reverse is also true. Suppressing the first event always suppresses the effect. Otherwise both events could be the effects of a third event as described for the corrosion example, or the alcohol example in Chapter One.
A mechanism must also be established. We can correlate many factors, but unless there is a viable explanation of how the two factors are related, then the relationship should be presumed to be casual and not causative, no matter how strong the correlation.
In the same way that we cannot describe the entire universe, the real world is much too complex to comprehend in complete and exact detail. Consequently, we must simplify the real situation by abstracting certain aspects that make up an idealized version of the real event. This idealization, if successful, provides a useful approximation to the real situation.
It is often convenient to simplify matters further by breaking the idealization into a number of parts, for the purposes of analysis. The possibility of doing this depends upon whether there are parts which are approximately independent of one another, or that there be only simple interactions. For example, when we study the human body, it is common to separate functions such as the respiratory, circulatory, and nervous and digestive systems, even though they are not completely independent.
At the same time that we idealize real events, we usually try to simplify them. Common examples are when researchers simplify complex phenomenon using a statistical model—such as models of travel behavior. In adopting these simplifications, we must be cognizant of the fact we may have oversimplified events such that our model no longer represents real world behavior, and in fact is missing some key elements of the causal process.
When the parts of a problem have been solved, we may be able to synthesize the simple parts and construct an approximation of the real situation. The validity of the model must be established by observation or the ability to predict events. For these techniques to be successful, it is essential that the parts chosen be the right ones and that interactions be sufficiently taken into account. The techniques of analysis and synthesis are not appropriate where complex interactions exist.
Induction, Deduction, and Abduction
Induction, or generalization, is the basic method for drawing conclusions from scientific inquiries. This is the process of drawing inferences about a whole class from observations of a few of its members. For example, when a biologist describes the characteristics of an insect, he is not primarily interested in the characteristics of the insect under observation, but in those characteristics he believes are shared by all other insects of the same species. Or, if an engineer observes defects in the bituminous pavement, he is interested not only in the specific deficiencies but also whether other pavements built at the same time with similar materials may also exhibit the same types of deficiencies.
The inductive method of reasoning has been used for a long time, but it is not foolproof. We must be aware that the human mind is very creative, and may establish generalizations, some of which become widely accepted, that cannot be substantiated. For example, countless generations of arthritis sufferers have believed that the severity of their pain was affected by the weather. A study reported in 1996 showed that there is no correlation between the two. The researchers concluded, “We hypothesize that this belief results, in part at least, from people’s tendency to perceive patterns where none exist” (7).
There are a number of pitfalls in the method of inductive reasoning that must be avoided. Because it is not practical to examine every member of a class, induction is based on the study of part, or a sample, of the class. It is important that bias not be introduced into the sample, and the best way to avoid sampling errors is to use the random method of sampling. Random sampling also permits confidence limits to be placed on the statement and establish the probability of it being correct. There are also some general rules about the validity of inductive statements. The first is that the more precisely a class can be specified, the more likely it is that the properties of individual members will be shared by the whole class. The second is that the more varied the conditions under which the property is observed, the stronger the evidence for the generalizations. Thirdly, if the observations are in accordance with a theory, the generalization is strengthened. The contrary is also true, i.e. purely empirical generalizations are not highly regarded until an explanation or theory exists.
Finally, Wilson (1) makes the point that no generalization is ever completely true, and that few generalizations based on many data are completely false. No matter how carefully and completely a class is defined, an individual member eventually turns up which contradicts the generalization. This does not usually lead to outright rejection of the generalization, but to a more precise definition of the class and new limitations on the generalization.
Deduction is the logical reasoning that something must be true because it is a particular case of a general statement that is known to be true. This technique also provides a method for the testing of hypotheses. While it may be difficult to test a hypothesis directly, we may deduce that, for the hypothesis to be true, there are a number of consequences that can be tested directly. If the consequences are proven true, this adds credence to the hypothesis. The principles of deductive logic can be expressed mathematically by means of a symbolic notation, hence the name symbolic logic. Mathematics makes possible much more complex and far-reaching deductions than would be possible if argued in ordinary language.
Abduction, in contrast to induction and deduction, is not symbolic logic but critical thinking. Abduction is to look for a pattern in a phenomenon and suggest a hypothesis (20). Despite the long history of abduction, abduction remains unpopular among texts of logic and research methodology, which emphasize formal logic. Logic is divided into formal types of reasoning (symbolic logic) and informal types (critical thinking). Unlike deduction and induction, abduction is a type of critical thinking rather than symbolic
Logic. The following example illustrates the process of abduction:
The surprising phenomenon or outcome, X, is observed.
Among hypotheses A, B, and C, A is capable and logical for explaining X.
Hence, there is a reason to further test hypothesis A.
Humans find hypotheses much easier to understand if they can draw analogies with other phenomena, which they do understand. This desire to describe phenomena in terms of familiar concepts has led to the development of models. Models are very common in science and engineering, for example models of crystal structure, strength of materials, and in the analysis of the behavior of structures. In some cases we may not use a physical model, instead relying on a mathematical model or formula. We recognize that all models have limitations, but, for most people, they are the easiest way to understand behavior and appreciate the implications of theory.
In determining the validity of a hypothesis, it is important to define the conditions under which it is applicable. This involves defining conditions, which are necessary, and those, which are sufficient.
A necessary condition is one, which must be satisfied for a statement to be true, but there may be other conditions, which also must be satisfied.
A sufficient condition is one, which will ensure the truth of a statement, but there may be other conditions, which will also ensure the truth of the statement.
Defining the necessary and the sufficient conditions determines the minimum criteria that must be satisfied for a statement to be valid, which is extremely important.
The concept is explained most easily through a simple mathematical example. The condition that a number ends in 0 is sufficient to prove that the number is divisible by 5, but it is not necessary. Similarly, the condition that a number ends in 5 is also a sufficient condition. However, 0 and 5 are the only last digits, which will ensure that a number is divisible by 5. Therefore, the necessary and sufficient conditions for a number to be divisible by 5 are that it ends in either 0 or 5.
Another example can be used to reinforce the importance of the concept. A plant needs carbon dioxide, light, water, and nutrients to survive. All the conditions are necessary, but none is sufficient to ensure survival. The condition of sufficiency requires that all four conditions be satisfied. Thus we can say that the necessary and sufficient conditions for the survival of a plant are that carbon dioxide, light, water, and nutrients be available. If we had carbon dioxide, light, water, nutrients and soil, the plant would still survive, but we have not defined the necessary and sufficient conditions because the soil is not necessary.
Sound thinking and logical reasoning are necessary for successful scientific inquiry. Certain types of errors and false arguments, some of which have already been discussed in this chapter, are sufficiently common to be worth highlighting. Some false arguments are not easily spotted, and often, are not the result of fraudulent intent.
Circular logic or reasoning occurs when the alleged proof of a hypothesis contains one of the initial assumptions. A similar situation occurs when a researcher attempts to use the same set of data to validate a model, as was used to calibrate it.
The necessary conditions for cause and effect have been discussed in detail. Simply because two factors are related, does not mean that one is the cause of the other. Further, the fact that two events are related does not mean that the converse is true. For example, because a plant deprived of water will wilt, does not mean that all plants, which wilt, are short of water.
Just as luck and serendipity can have a very positive outcome in science, many incorrect conclusions are drawn because the possibility of chance occurrences is not considered sufficiently. This usually arises through lack of proper controls and insufficient repetitions.
Bias is responsible for much incorrect work. This may be blatant, as when the researcher’s reputation is based on a certain finding, or there are vested interests, or it may be subtle and unintentional, such as wishing for a positive outcome from an experiment. Safeguards against bias have already been discussed but perhaps the most important, is the need for an inquiring mind, which constantly challenges our current thinking and ideas. The human ego is very strong, and even critical thinkers can sometimes have difficulty accepting that they might make mistakes.
Another obstacle to good science is the entrapment argument for sustaining a project. This occurs when so much time and money have been invested in a study, that this becomes the rationale for continuation of the project. The researcher cannot afford to become so emotionally attached to a project that his judgement is clouded, and evidence of impending failure is overlooked. The entrapment argument can be avoided by practicing the management controls described in Chapter Three.
This page intentionally left blank.