A
ALPHABETICAL GLOSSARY OF USEFUL STATISTICAL AND RESEARCH RELATED TERMS
Abscissa: The horizontal or x-coordinate of a data point as graphed on a Cartesian coordinate system. The y-coordinate is called the ordinate.
Abduction: Abduction is to look for a pattern in a phenomenon and suggest a hypothesis. (Peirce, 1878. How to make our ideas clear. Popular Science Monthly, 12, 286-302) It is not symbolic logic but critical thinking, and is the only logical operation that can introduce a new idea.
Accuracy: Degree to which some estimate matches the true state of nature.
Aggregate: The value of a single variable that summarizes, adds, or represents the mean of a group or collection of data.
Aggregation: The compounding of primary data, usually for the purpose of expressing them in summary form.
Alpha level: Alpha is the probability assigned by the analyst that reflects the degree of acceptable risk for rejecting the null hypothesis when in fact the null hypothesis is true. The degree of risk is not interpretable for an individual event or outcome, instead it represents the long-run probability of making a type I error. See type I error.
Alternative Hypothesis: The hypothesis, which one accepts when the null hypothesis (the hypothesis under test) is rejected. It is usually denoted by HA or H1. Also see null hypothesis.
ANOVA: Analysis of Variance. The analysis of the total variability of a set of data (measured by their total sum of squares) into components that can be attributed to different sources of variation. The sources of variation include those caused by random fluctuations, and those caused by systematic differences between groups.
ANOVA table: A table that lists the various sources of variation together with the corresponding degrees.
Applied research: Original work undertaken to acquire new knowledge with a specific practical application in view. Applied research is undertaken to determine possible uses for the findings of basic research or to determine new methods or ways of achieving some specific and pre-determined objective.
Approximation error: In general, an error due to approximation from making a rough calculation, estimate, or guess. In numerical calculations, approximations result from rounding errors, for example P » 22/7 » 3.1417.
Arithmetic mean: The result of summing all measurements from a population or sample and dividing by the number of population or sample members. The arithmetic mean is also called the average, which is a measure of central tendency.
Association: The inclination of two events to occur simultaneously. Two variables that are associated are correlated, whereas two variables that are not associated (independent) are said to be uncorrelated. Association does not imply causation, whereas causation does imply association. Statistical evidence alone can be used to demonstrate association; however, causation must be established using strict experimental design, logic, and statistical evidence.
Attribute: A qualitative characteristic, as distinct from a variable or quantitative characteristic.
Attitude survey: Attitude surveys are individually designed to provide reliable and valid information to assist in making critical decisions to focus resources where they are most needed.
Auto-correlation: The temporal association between observations of a series of observations ordered across time.
ARIMA: See Autoregressive integrated moving average.
ARMA: See Autoregressive moving average.
Autoregressive integrated moving average (ARIMA) processes: Time series that can be made stationary by differencing and whose differenced observations are linearly dependent on past observations and past innovations.
Autoregressive moving average (ARMA) processes: Stationary time series whose observations are linearly dependent on past observations and past innovations.
Autoregressive (AR) Processes: Stationary time series that are characterized by a linear relationship between adjacent observations. The order of the process p defines the number of past observations on which the current observation depends.
Average: The arithmetic mean of a set of observations. The average is a measure of central tendency of a scattering of observations, as is also the median and mode.
B
Backshift operator: Model convention that defines stepping backward in a time-indexed data series.
Bar chart or diagram: A graph of observed data using a sequence of rectangles, whose widths are fixed and whose heights are proportional to the number of observations, proportion of total observations, or probability of occurrence.
Basic research: The undertaking of research with the aim of advancing the current state of knowledge and to develop an understanding of a fundamental or basic process, phenomenon, material, or event.
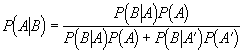
Bayes’ theorem: This theorem, developed by Bayes, is a theorem that relates the conditional probability of occurrence of an event to the probabilities of other events. Bayes’ theorem is given by:
where P (A|B) is the probability of event A given that event B has occurred, P (A) is the probability of event A, and P (A’) is the probability of event A not occurring. Bayes’ theorem can be used to overcome some of the interpretive and philosophical shortcomings of frequentist or classical statistical methods.
Bayesian philosophy: Bayesian statisticians base statistical inference on a number of philosophical underpinnings that differ in principle to frequentist or classical statistical thought. First, Bayesians believe that research results should reflect updates of past research. In other words, prior knowledge should be incorporated formally into current research to obtain the best ‘posterior’ or resultant knowledge. Second, Bayesians believe that much can be gained from insightful prior, subjective information as to the likelihood of certain types of events. Third, Bayesians use Bayes’ theorem to translate probabilistic statements into degrees of belief, instead of a classical confidence interval interpretation. Bayesian methods essentially introduce (mathematically) subjective prior information into the analysis framework.
Before-after study: A study wherein data are collected prior to and following an event, treatment, or action. The event, treatment, or action applied between the two periods is thought to affect the data under investigation. The purpose of this type study is to show a relationship between the data and the event, treatment, or action. In experimental research all other factors are either randomized or controlled.
Bernoulli distribution: Another name for Binomial distribution.
Bernoulli trial: An experiment where there is a fixed probability p of “success”, and a fixed probability 1 – p of “failure”. In a Bernoulli process, the events are independent of one another from trial to trial.
Best Fit: See Goodness of Fit.
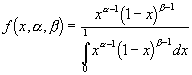
Beta Distribution: A distribution, which is closely related to the F-Distribution, used extensively in analysis of variance. In Bayesian inference, the beta distribution is sometimes used as the prior distribution of a parameter of interest. The beta distribution, when used to describe the distribution of lambda of a mixture of Poisson distributions, results in the negative binomial distribution. The beta distribution is given by:
where a and b are shape parameters, the mean is a / (a + b), and variance is ab / [(a + b +1)(a + b)].
Beta coefficients: The coefficients in statistical models, often represented by the Greek letter b. Beta coefficients are meant to represent fixed parameters of the population, whereas estimates of betas, typically represented by b, are computed from the sample.
Beta error: Beta is a probability assigned by the analyst that reflects the degree of acceptable risk for accepting the null hypothesis when in fact the null hypothesis is false. The degree of risk is not interpretable for an individual event or outcome, instead it represents the long-run probability of making a type II error .See also Type II error.
Bias: In problems of estimation of population parameters, an estimator is assumed biased if its expected value does not equal the parameter it is intended to estimate. In sampling, a bias is a systematic error introduced by selecting items non-randomly from a population that is assumed to be random. A survey question can be biased if it is poorly phrased. Also see unbiased.
![]()
Binomial Distribution: The distribution of the number of successes in n trials, when the probability of success (and failure) remains constant from trial to trial and the trials are independent. It is also known as Bernoulli distribution or process, and is given by:
where x is the number of “successes” out of n trials, p is the probability of success, and ! represents the factorial operator, such that 3! = 3 x 2 x 1.
Bivariate distribution: A bivariate distribution is the distribution resulting from two random variables. For instance, the distribution of vehicle model year (MY) by annual mileage (AM) driven. If MY and AM are independent variables, then the bivariate distribution will be approximate uniform across cells. Since older vehicles are driven less per year on average then newer vehicles, these two variables are dependent, that is, annual mileage is dependent upon model year. A contingency table, or cross classification analysis is useful for testing statistical independence among two or more variables.
Block Diagram: Consists of vertically placed rectangles on a common base line, usually the height of the rectangles being proportional to a quantitative variable.
C
Categorical variable: A categorical or nominal scale variable has no particular ordering, and intervals between these variables are without meaning. Examples of categorical variables include vehicle manufacturer. For a categorical variable to be used appropriately it must be mutually exclusive and collectively exhaustive.
Causation: When event A causes event B, there exists a material, plausible, underlying reason or explanation relating event B with event A. Causality cannot be proved with statistics, merely strong evidence in support of a causal relation can be asserted. Causality is more defensible as the result of statistical evidence obtained from designed experiments, whereas data obtained from observational and quasi-experiments are implied as correlated or associated.
Censored distribution: A censored statistical distribution occurs when a response above or below a certain threshold value is fixed at that threshold. For instance, for a stadium that holds 50,000 seats, the number of tickets sold cannot exceed 50,000, even though there might be a demand for greater than 50,000 seats.
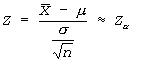
Central limit theorem: If xave is calculated on a sample drawn from a distribution with mean m and known finite variance s2, then the sampling distribution of the test statistic Z is approximately standard normal distributed, regardless of the characteristics of the parent distribution (i.e. normal, Poisson, binomial, etc.). Thus, a random variable Z computed as follows is approximately standard normal (mean=0, variance=1) distributed:
The distribution of random variable Z approaches that of the standard normal distribution as n approaches infinity.
Central Tendency: The tendency of quantitative data to cluster around some variate value.
![]()
Chebyshev’s inequality: A useful theorem, which states that for a probability distribution with mean m and standard deviation s, the probability that an observation drawn from the distribution differs from m by more than ks is less than 1/k2, or stated mathematically:
Chi-squared distribution: This distribution is of great importance for inferences concerning population variances or standard deviations, and for comparing two distributions of any type. It arises in connection with the sampling distribution of the sample variance for random samples from normal populations. If s2 is the estimated variance of a random sample of size n drawn from a normal population having variance s2, then the sample distribution of the test statistic X2 is approximately chi-square distributed with n = n – 1 degrees of freedom:
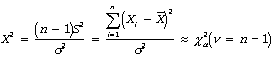
![]()
Chi-squared statistic: The chi-squared statistic is used for comparisons between observed cell frequencies in an empirical (observed) distribution and expected frequencies under a hypothesized (theoretical or other observed) distribution. The statistic is used to assess evidence that two distributions are dissimilar, and is given by:
where, X2 is the computed test statistic, I is the number of classes or intervals in a frequency histogram, fi is the observed frequency in histogram class I=i, fi (0) is the expected frequency in histogram class I=i under the hypothesized distribution, and c2a is the critical value of the chi-square distribution with (I-1) degrees of freedom and level of significance alpha.
Class: Observations grouped according to convenient divisions of the variate range, usually to simplify subsequent analysis (the upper and lower limits of a class are called class boundaries; the interval between them the class interval; and the frequency falling into the class is the class frequency).
Cluster sampling: A type of sampling whereby observations are selected at random from several clusters instead of at random from the entire population. It is intended that the heterogeneity in the phenomenon of interest is reflected within the clusters, i.e., members in the clusters are not homogenous with respect to the response variable. Cluster sampling is less satisfactory from a statistical standpoint, but often can be more economical and/or practical.
Coefficient of determination: Employed in ordinary least squares regression and denoted R2, the coefficient of determination is the proportion of total variance in the data taken up or ‘explained’ by the independent variables in the regression model. It is the ratio or proportion of explained variance to total variance and is bounded by 0 and 1 for models with intercept terms. Because adding explanatory variables to a model cannot reduce the value of R2, and adjusted R2 is often used to compare models with different numbers of explanatory variables. The value of R2 from a model can not be evaluated as “good” or “bad” in singularity, it can only be judged relative to other models that have been estimated on similar phenomenon—thus an R2 of 30% for some phenomenon may be extremely informative, while for other phenomenon might be uninformative.
Collectively exhaustive: When a categorical variable is collectively exhaustive it represents all possible categories that a random variable may fall into.
Conditional probability: Conditional probability is the long run likelihood that an event will occur given that a specific condition has already occurred, e.g. the probability that it will rain today, given that it rained yesterday. The standard notation for conditional probability is P (A|B), which corresponds to the probability that event A occurs given the event B has already occurred. It can also be shown that:
![]()
where P (A Ç B) is the probability that both event A and B occur.
Confidence interval: A confidence interval is a calculated range of values known to contain the true parameter of interest over the average of repeated trials with specific certainty (probability). The correct interpretation of a confidence interval is as follows: If the analyst were to repeatedly draw samples at the same levels of the independent variables and compute the test statistic (mean, regression slope, etc.), then the true population parameter would lie in the (1-a)% confidence interval a times out of 100.
Confidence coefficient: The measure of probability a (see alpha error) associated with a confidence interval that the interval will include the true population parameter of interest.
Confidence region: A region or interval in the parameter space such that there will be an assigned confidence level a that the true population parameter lies within the interval or region.
Confounded variables: A confounded variable generally refers to a variable in a statistical model that is correlated with a variable that is not included in a model. Sometimes called an omitted variable problem, when variables in a model are correlated with variables excluded from a model then the estimates of parameters in the model are biased. The direction of bias depends upon the correlation between the confounded variables. In addition, the estimate of model error is also biased.
![]()
Consistent: An estimate of a population parameter, such as the population mean or variance, obtained from a sample of observations is said to be consistent if the estimate approaches the value of the true population parameter as the sample size approaches infinity. Stated more formally:
where bhat are estimated parameters, b are true population parameters, n is sample size, and e is a positive small difference between estimated and true population parameters.
Contingency coefficient: A measure of the strength of the association between two variables, usually qualitative, on the basis of data tallied into a contingency table. The statistic is never negative, and has a maximum value less than 1, depending on the number of rows and columns in the contingency table.
Contingency table: Cross-classification is a statistical technique that relies on properties of the multinomial distribution, statistical independence, and the chi-square distribution to determine the strength of association (or lack thereof) between two or more factors or variables.
Continuous variable: A continuous variable is either measured on the interval or ratio scale. A continuous variable can theoretically take on an infinite number of values within an interval. Examples of continuous variables include measurements in distance, time, and mass.
Control Chart: A graphical device used to display the results of small scale, repeated sampling of a manufacturing process, usually showing the average value, together with upper and lower control limits between which a stated portion of the sample statistics should fall.
Control group: A control group is a comparison group of experimental units that do not receive the treatment, and can be used to compare to the experimental group with respect to the phenomenon of interest.
Correlation: This term denotes the relationship (association or dependence) between two or more qualitative or quantitative variables. When two variables are correlated that are said to be statistically dependent, when they are uncorrelated they are said to be statistically independent. For continuous variables Pearson’s product moment correlation coefficient is often used, while for rank or ordinal data Kendall’s coefficient of rank correlation is used.
Correlation coefficient: A correlation coefficient is a measure of the interdependence between two variates or variables. For interval or ratio scale variables it is a fraction, which lies between –1 for perfect negative correlation, and 1 for perfect positive correlation. An intermediate value of zero indicating the absence of correlation, but not necessarily independence of the variates or variables, since the observed correlation could have been observed by chance fluctuations.
Correlation matrix: For a set of variables X1… Xn, with correlation between Xi and Xj denoted by rij, the correlation matrix is a square symmetric matrix with values rij.
Covariance: The expected value of the product of the deviations of two random variables from their respective means i.e. E [(X1-m1)( X2-m2)] = åi =1 to n [(X1i-m1)( X2i-m2)]/n. Correlation and covariance are related statistics in that the correlation is the standardized form of the covariance, that is, covariance is a measure of the association in original units, whereas the correlation is the measure of association in standardized units.
Cross-sectional data: Data collected on some variable, at the same point or during a particular period of time, from different geographical regions, organizations, households, etc. (contrast this to time series data).
D
Data: Information or measurements obtained from a survey, experiment, investigation, or observational study. Data are stored in a database, usually in electronic form.
Deduction: The logical reasoning that something must be true because it is a particular case of a general statement that is known to be true. Deduction cannot lead to new knowledge.
Demonstration: Limited scale application to establish and communicate the viability and practicality of a new product, process or practice.
Dependent variables: If a function is given by Y = f (X1,………. Xn), it is customary to refer to X1,………. Xn as independent or explanatory variables, and Y as the dependent or response variable. The majority of statistical investigations in transportation aim to predict or explain values (or expected values) of dependent variables given known or observed values of independent variables.
Degrees of freedom: Degrees of freedom are the number of free variables in a set of observations used to estimate statistical parameters. For instance, the estimation of the population standard deviation computed on a sample of observations requires an estimate of the population mean, which consumes one degree of freedom to estimate—thus the sample standard deviation has n-1 degrees of freedom remaining. The degrees of freedom associated with the error around a linear regression function has n-2 degrees of freedom, since two degrees of freedom have been used to estimate the slope and intercept of the regression line.
Descriptive statistics: Statistics used to display, describe, graph, or depict data. Descriptive statistics do not generally include modeling of data.
Deterministic model or process: A deterministic model, as opposed to a stochastic model, is one which contains effectively no or negligible random elements and for which, therefore, the future course of the system can be completely determined by its position, velocities, etc. An example of a deterministic model is given by Force = Mass x Acceleration.
Development: A process of arriving at a satisfactory design of a viable application of new knowledge by employing sequential cycles of designing, testing, and evaluating.
Discrete variable: A discrete variable is measured on the nominal or ordinal scale, and can assume a finite number of values within an interval or range. Discrete variables are less informative than are continuous variables.
Dispersion: The degree of scatter or concentration of observations around its center or middle. Dispersion is usually measured as a deviation about some central value such as the mean, standard, or absolute deviation, or by an order statistic such as deciles, quintiles, and quartiles.
Distribution: The set of frequencies or probabilities assigned to various outcomes of a particular event or trial.
Distribution function: The function, denoted F (x), which gives the cumulative frequency or probability that random variable X takes on a value less than or equal to x.
E
Econometrics: The development and application of statistical and/or mathematical principles and techniques for solving economic problems.
Effectiveness: The quantity of product or services consumed per unit cost or resource to produce them.
Efficiency (non-statistical): Unit input resources required per unit output (see also productivity).
Efficiency (statistical): A statistical estimator or estimate is said to be efficient if it has small variance. In most cases a statistical estimate is preferred if it is more efficient than alternative estimates. It can be shown that the Cramer-Rao bound represents the best possible efficiency (lowest variance) for an unbiased estimator. That is, if an unbiased estimator is shown to be equivalent to the Cramer-Rao bound, then there are no other unbiased estimators that are more efficient. It is possible in some cases to find a more efficient estimate of a population parameter that is biased.
Empirical: Derived from experimentation or observation rather then underlying theory.
Engineering: The science of applying knowledge of the physical, chemical, and electrical properties of static and dynamic matter to the practical problems of society and the surrounding environment.
Error: In a statistical interpretation the word ‘error’ is used to denote the difference between an observed value and its ‘expected’ value as predicted or explained by a model. In addition, errors occur in data collection, sometimes resulting in outlying observations. Finally, type I and type II errors refer to specific interpretive errors made when analyzing the results of hypothesis tests.
Error mean square: In analysis of variance and regression, the error mean square often called the mean square error (MSE) is the residual or error sum of squares divided by its degrees of freedom. It provides an estimate of the residual or error variance of the population from which the sample was drawn.
Error of Observation: An error arising from imperfections in the method of observing a quantity, whether due to instrumental or to human factors
Error variance: The variance of the random or unexplainable component of a model; the term is used mainly in the presence of other sources of variation, as for example in regression analysis or in analysis of variance.
Error rate: In hypothesis testing, the error rate is the unconditional probability of making an error; that is, erroneously accepting or rejecting a statistical hypothesis. Note that the probabilities of Type I and Type II errors, alpha and beta, are conditional probabilities, the first is subject to the condition that the null hypothesis is true, and the second is subject to the condition that the null hypothesis false.
Ethics: Moral principles on which decisions and actions are based.
Experiment: A set of measurements carried out under specific and controlled conditions to discover, verify, or illustrate a theory, hypothesis, or relationship. Experiments are the cornerstone of statistical theory, and are the only method for suggesting causal relations between variables. Experimental hypotheses cannot be proved using statistics; however, they can be disproved. Elements of an experiment generally include a control group, randomization, and repeat observations.
Experimental data: Data obtained by conducting experiments under controlled conditions is called experimental data. Quasi-experimental data are obtained when some factors are controlled as in an experiment, but some factors are not. Observational data are obtained when no exogenous factors other than the treatment are controlled or manipulated. Analysis and modeling based on quasi-experimental and observation data are subject to illusory correlation and confounding of variables.
Experimental design: Plan or blueprint for conducting an experiment.
Experimental Error: Any error in an experiment whether due to stochastic variation or bias (not including mistakes in design or avoidable imperfections in technique).
Exploratory research: Exploratory research is synonymous with data mining. It is research undertaken with the intent to uncover previously undiscovered relationships in data. Unfortunately, data mining leads to a higher likelihood of illusory correlation, omitted variable bias, and post-hoc theorizing, all of which threaten high-quality research and scientific investigations. Exploratory research should be undertaken with great caution, and conclusions drawn from it should be made with sufficient caveats and pessimism.
Exogenous variables: An exogenous variable in a statistical model refers to a variable whose value is determined by influences outside of the statistical model. An assumption of statistical modeling is that explanatory variables are exogenous. When explanatory variables are endogenous, problems arise when using these variables in statistical models.
Expectation: The expected or mean value of a random variable, or function of that variable such as the mean or variance.
Exponential: A variable raised to a power of x. The function F (x) = ax is an exponential function.
![]()
Exponential distribution: The exponential distribution is a continuous distribution, and is typically used to model life cycles or decay of materials or events. Its probability density function given by:
Exponential smoothing: Time series regression in which recent observations are given more weight by way of exponentially decaying regression coefficients.
F
F-distribution: The F distribution is of fundamental importance in analysis of variance and regression. If s12 and s22 are the variances of independent random samples of size n1 and n2 respectively, then the sampling distribution of the test statistic F is approximately F distributed with n1 (numerator) and n1 (denominator) degrees of freedom such that:
![]()
F-test: A computed statistic, which under an appropriate null hypothesis has an approximate F-Distribution.
F Ratio: The ratio of two independent unbiased estimates of variance of a normal distribution; has widespread application in the analysis of variance.
Factorial Experiment: An experiment designed to examine the effect of one or more factors, each factor being applied at two levels at least so that different effects can be observed.
Full Factorial Experiment: An experiment investigating all the possible treatment combinations that may be formed from the factors under investigation.
Frequency: The number of occurrences of a given type of event.
G
Gamma distribution: The Gamma distribution includes as special cases the chi-square distribution and the exponential distribution. It has many important applications; in Bayesian inference, for example, it is sometimes used as the a priori distribution for the parameter (mean) of a Poisson distribution. The gamma distribution is given by:
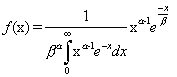
where alpha and beta are shape parameters. The mean and variance of the gamma distribution are m = ab and s2 = ab2 respectively.
Gantt Chart: A bar chart showing actual performance or output expressed as a percentage of a quota or planned performance per unit of time.
Gaussian distribution: The guassian distribution is another name for the normal distribution.
Goodness of Fit: Goodness of fit describes a class of statistics used to assess the fit of a model to observed data. There are numerous goodness of fit measures, including the coefficient of determination R2, the F-test, the chi-square test for frequency data, and numerous other measures. It should be noted that goodness might refer to the fit of a statistical model to data used for estimation, or data used for validation.
H
Heterogeneity: This term is used in statistics to describe samples or individuals from different populations, which differ with respect to the phenomenon of interest. If the populations are not identical they are said to be heterogeneous, and by extension, the sample data is also said to be heterogeneous.
Heteroscedasticity: In regression analysis, the property that the conditional distributions of the response variable Y for fixed values of the independent variables do not all have constant variance. Non-constant variance in a regression model results in inflated estimates of model mean square error. Standard remedies include transformations of the response, and/or employing a generalized linear model.
Histogram: A univariate frequency diagram in which rectangles proportional in area to the class frequencies are erected on sections of the horizontal axis, the width of each section representing the corresponding class interval of the variate.
Holt-Winters smoothing: A seasonal time series modeling approach in which the original series is decomposed into its level, trend, and seasonal components with each of the components being modeled with exponentially smoothed regression.
Homogeneity: This term is used in statistics to describe samples or individuals from populations, which are similar with respect to the phenomenon of interest. If the populations are similar they are said to be homogenous, and by extension, the sample data is also said to be homogenous.
Homoscedasticity: In regression analysis, the property that the conditional distributions of Y for fixed values of the independent variable all have the same variance. See also Heteroscedasticity.
Hypothesis: A statistical hypothesis is a hypothesis concerning the value of parameters or form of a probability distribution for a designated population or populations. More generally, a statistical hypothesis is a formal statement about the underlying mechanisms that generated some observed data.
Hypothesis testing: A term used to refer to testing whether observed data support a stated position or hypothesis. Support of a research hypothesis suggests that the data would have been unlikely if the hypothesis were indeed false. See also type I and type II errors.
I
Illusory correlation: Illusory correlation is an omitted variable problem, similar to confounding. Illusory correlation is used to describe the situation where Y and X1 are correlated, yet the relation is illusory, because X1 is actually correlated with X2, which is the true ‘cause’ of changes in Y.
Independent events: In probability theory, two events are said to be statistically independent if, and only if the probability that they will both occur equals the product of the probabilities that each one, individually will occur. Independent events are not correlated, whereas dependent events are. See also dependence and correlation.
Independent variables: Two variables are said to be statistically independent if, and only if the probability that they will both occur equals the product of the probabilities that each one, individually will occur. Independent events are not correlated, whereas dependent events are. See also dependence and correlation.
Indicator variables: Indicator variables are used to quantify the effect of a qualitative or discrete variable in a statistical model. Also called dummy variables, indicator variables typically take on values of zero or one. Indicator variables are coded from ordinal or nominal variables. For a nominal variable with n levels, n-1 indicator variables are coded for use in a statistical model. For instance, the nominal variable Vehicle Type: truck, van, or auto, the analyst would code X1 = 1 for truck, 0 otherwise and X2 = 1 for van, 0 otherwise. When both X1 and X2 are coded as zero, the respondent was an auto.
Induction: The process of drawing inferences about an entire class based upon observations on a few of its members.
Information criteria: Model performance measures that balance decreases in model error with increase in model complexity. In general, information criteria are based on the Gaussian likelihood of the model estimates with a penalty for the number of model parameters.
Innovation: To make changes, introduce new practices, etc. Research can be innovative, in that it uncovers or introduces new relationships that previously were not known, by applying statistical techniques that offer new insights into data, or by developing testable hypothesis that have previously not been postulated or tested.
Innovation series: The zero-mean uncorrelated stochastic component of a time series that remains after all deterministic and correlated elements have been appropriately modeled. The innovations are also referred to as the series noise.
Interaction: Two variables X1 and X2 are said to interact if the value of X1 influences the value of X2 positively or negatively. An interaction is a synergy between two or more variables, and reflects the fact that their combined effect on a response not only depends on the level of the individual variables, but their combined levels as well.
Interval Estimate: The estimation of a population parameter by specifying a range of values bounded an upper and lower limit, within which the true value is asserted to lie.
Interval scale: The interval measurement scale has equal differences between pairs of points anywhere on the scale, but the zero point is arbitrary. An example interval scale is the time scale in years, 1 A.D., 2, 3,……1999. Each interval on the scale represents a single year, or 365 days; however, time did not begin at time 0. The ratio scale variable provides the statistician with the second greatest amount of information relative to other scales of measurement. See also nominal, ordinal, and ratio scales.
Interviewer Bias: Bias in responses, or recorded information, which is the direct result of the action of the interviewer.
J
Joint probability: The joint probability is the joint density function of two random variables, or bivariate density.
K
Kendall’s coefficient of rank correlation: Denoted as tij, where i and j refer to two variables, Kendall’s coefficient of rank correlation reflects the degree of linear association between two ordinal variables, and is bounded between +1 for perfect positive correlation and –1 for perfect negative correlation. The formula for tij is given by:
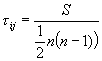
where S is the sum of scores (see non-parametric statistic reference for computing scores) and n is sample size.
L
Least squares estimation: A technique of estimating statistical parameters from sample data whereby parameters are determined by minimizing the squared differences between model predictions and observed values of the response. The method may be regarded as possessing an empirical justification in that the process of minimization gives an optimum fit of observation to theoretical models; but for restricted cases such as normal theory linear models, estimated parameters have optimum statistical properties of unbiasedness and efficiency.
Level of significance: The level of significance is the probability of rejecting a null hypothesis, when it is in fact true. It is also known as a , or the probability of committing a Type I error.
Likelihood function: The probability or probability density of obtaining a given set of sample values, from a certain population, when this probability or probability density is regarded as a function of the parameter(s) of the population and not as a function of the sample data. See also maximum likelihood method.
Linear correlation: A somewhat ambiguous expression used to denote either (a) Pearson’s Product Moment Correlation in cases where the corresponding variables are continuous, or (b) a Correlation Coefficient on ordinal data such as Kendall’s Rank Correlation Coefficient. There are other linear correlation coefficients besides the two listed here as well.
Linear model: A mathematical model in which the equation relating the random variables and parameters are linear in parameters. Although the functional form of the model Y = a + b1 X1+ b2 X12 includes the non-linear term b2X12, the model itself is linear, because the statistical parameters are linearly related to the random variables.
Lot: A group of units produced under similar conditions.
M
Maximum likelihood method: A method of parameter estimation in which a parameter is estimated by the value of the parameter that maximizes the likelihood function. In other words, the maximum likelihood estimator is the value of theta that maximizes the probability of the observed sample. The method can also be used for the simultaneous estimation of several parameters, such as regression parameters. Estimates obtained using this method are called maximum likelihood estimates.
Mean: That value of a variate such that the sum of deviations from it is zero, and thus it is the sum of a set of values divided by their number.
Mean square error: For unbiased estimators, the mean square error is an estimate of the population variance, and is usually denoted MSE. For biased estimators, the mean squared deviation of an estimator from the true value is equal to the variance plus the squared bias. The square root of the mean square error is referred to as the root mean square error.
Median: The median is the middle most number in an ordered series of numbers. It is a measure of central tendency, and is often a more robust measure of central tendency, that is, the median is less sensitive to outliers than is the sample mean.
Mode: The mode is the most common or most probable value observed in a set of observations or sample.
Model: A model is a formal expression of a theory or causal or associative relationship between variables, which is regarded by the analyst as having generated the observed data. A statistical model is always a simplified expression of a more complex process, and thus, the analyst should anticipate some degree of approximation a priori. A statistical model that can explain the greatest amount of underlying complexity with the simplest model form is preferred to a more complex model.
Moving average (MA) processes: Stationary time series that are characterized by a linear relationship between observations and past innovations. The order of the process q defines the number of past innovations on which the current observation depends.
Multi-collinearity: Multi-collinearity is a term used to describe when two variables are correlated with each other. In statistical models, multi-collinearity causes problems with the efficiency of parameter estimates. It also raises some philosophical issues, since it becomes difficult to determine which variables (both, either, or none), are causal and which are the result of illusory correlation.
Multiple linear regression: A linear regression involving two or more independent variables. Simple linear regression, which is merely used to illustrate the basic properties of regression models, contains one explanatory variable and is rarely if ever used in practice.
Mutually exclusive events: In probability theory, two events are said to be mutually exclusive if and only if they are represented by disjoint subsets of the sample space, namely, by subsets that have no elements or events in common. By definition the probability of mutually exclusive events A and B occurring is zero.
N
Noise: A convenient term for a series of random disturbances, or deviation from the actual distribution. Statistical noise is a synonym for error term, disturbance, or random fluctuation.
Nominal scale: A variable measured on a nominal scale is the same as a categorical variable. The nominal scale lacks order and does not posses even intervals between levels of the variable. An example of a nominal scale variable is Vehicle Type, where levels of response include truck, van, and auto. The nominal scale variable provides the statistician with the least amount of information relative to other scales of measurement. See also ordinal, interval, and ratio scales of measurement.
Non-linear relation: A non-linear relation is one where a scatter plot between two variables X1 and X2 will not produce a straight-line trend. In many cases a linear trend can be observed between two variables by transforming the scale of one or both variables. For example, a scatter plot of log(X1) and X2 might produce a linear trend. In this case the variables are said to be non-linearly related in their original scales, but linear in transformed scale of X1.
Non-random sample: A sample selected by a non-random method. For example, a scheme whereby units are self-selected would yield a non-random sample, where units that prefer to participate do so. Some aspects of non-random sampling can be overcome, however
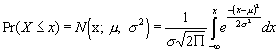
Normal distribution: A continuous distribution that was first studied in connection with errors of measurement and, thus, referred to as the ‘normal curve of errors.’ The normal distribution forms the cornerstone of a substantial portion of statistical theory. Also called the Gaussian distribution, the normal distribution has the two parameters m and s; when m = 0 and s = 1 it is said to be in its standard form, and it is referred to as the standard normal distribution. The normal distribution is characterized by its symmetric shape and bell-shaped appearance. The cumulative normal distribution density is given by:
Null hypothesis: In general, this term relates to a particular research hypothesis being tested, as distinct from the alternative hypothesis, which is accepted if the research hypothesis is rejected. Contrary to intuition, the null hypothesis is often a research hypothesis that the analyst would prefer to reject in favor of the alternative hypothesis, but this is not always the case. Erroneous rejection of the null hypothesis is known as a Type I error, whereas erroneous acceptance of the null hypothesis is known as a Type II error.
O
Observational Data: Observational data are non-experimental data, and there is no control of potential confounding variables in the study. Because of the weak inferential grounds of statistical results based on observational data, the support for conclusions based on observational data must be strongly supported by logic, underlying material explanations, identification of potential omitted variables and their expected biases, and caveats identifying the limitations of the study.
Omitted variable bias: Variables that affect the dependent variable that are omitted from a statistical model are problematic. Irrelevant omitted variables cause no bias in parameter estimates. Important variables that are uncorrelated with included variables will also cause no bias in parameter estimates, but the estimate of s2 is biased high. Omitted variables that are correlated with an included variable X1 will produce biased parameter estimates. The sign of the bias depends on the product of the covariance of the omitted variable and X1 and b1, the biased parameter. For instance, if the covariance is negative and b1 is negative, then the parameter will be biased positive. In addition, s2 is also biased.
One-tail test: Also known as a one-sided test, a test of a statistical hypothesis in which the region of rejection consists of either the right hand tail or the left hand tail of the sampling distribution of the test statistic. Philosophically, a one-sided tests represents the analyst’s a priori belief that a certain population parameter is either negative or positive.
Opinion: A belief or conviction, based on what seems probable or true but not demonstrable fact. The collective views of a large number of people, esp. on some particular topic. Much research has shown that individuals do not possess the skills to adequately assess risk or estimate probabilities, or predict the natural process of randomness. Thus, opinions can often be contrary to statistical evidence.
Ordinal scale: The ordinal scale of measurement occurs when a random variable can take on ordered values, but there is not an even interval between levels of the variable. Examples of ordinal variables include the choice between three automobile brands, where the response is highly desirable, desirable, and least desirable. Ordinal variables provide the second lowest amount of information compared to other scales of measurement. See also nominal, interval, and ratio scales of measurement.
Ordinary differencing: Creating a transformed series by subtracting the immediately adjacent observations.
Outliers: Outliers are identified as such because they “appear” to be outlying with respect to a large number of apparently similar observations or experimental units according to a specified model. In many cases outliers can be traced to errors in data collecting, recording, or calculation, and can be corrected or appropriately discarded. However, outliers can be so without a plausible explanation. In these cases it is usually the analyst’s omission of an important variable that differentiates the outlier from the remaining otherwise similar observations, or a mis-specification of the statistical model that fails to capture the correct underlying relationships. Outliers of this latter kind should not be discarded from the ‘other’ data unless they can be modeled separately, and their exclusion justified.
P
Parameter: This word occurs in its customary mathematical meaning of an unknown quantity that varies over a certain set of inputs. In statistical modeling, it most usually occurs in expressions defining frequency or probability distributions in terms of their relevant parameters (such as mean and variance of normal distribution), or in statistical models describing the estimated effect of a variable or variables on a response. Of utmost importance is the notion that statistical parameters are merely estimates, computed from the sample data, which are meant to provide insight as to what the true population parameter value is, although the true population parameter always remains unknown to the analyst.
![]()
Pearson’s product moment correlation coefficient: Denoted as rij, where i and j refer to two variables, Pearson’s product moment correlation coefficient reflects the degree of linear association between two continuous (ratio or interval scale) variables, and is bounded between +1 for perfect positive correlation and –1 for perfect negative correlation. The formula for rij is given by:
where sij is the covariance between variables i and j, and si and sj are the standard deviations of variables i and j respectively.
Pilot survey: A study, usually on a minor scale, carried out prior to the main survey, primarily to gain information about the appropriateness of the survey instrument, and to improve the efficiency of the main survey. Pilot surveys are an important step in the survey process, specifically for removing unintentional survey question biases, clarifying ambiguous questions, and for identifying gaps and/or inconsistencies in the survey instrument.
Point Estimate: The best single estimated value of a parameter.
![]()
Poisson distribution: The Poisson distribution is often referred to as the distribution of rare events. It is typically used to describe the probability of occurrence of an event over time, space, or length. In general, the Poisson distribution is appropriate when the following conditions hold: the probability of ‘success’ in any given trial is relatively small; the number of trials is large; and the trials are independent. The probability density function for the Poisson distribution is given as:
where, x is the number of occurrences per interval, l is the mean number of occurrences per interval, a is the mean rate of occurrence (occurrence per unit time, length, or space), DT is the interval length, and l = a DT.
Population: In statistical usage the term population is applied to any finite or infinite collection of individuals. It is important to distinguish between the population, for which statistical parameters are fixed and unknown at any given instant in time, and the sample of the population, from which estimates of the population parameters are computed. Population statistics are generally unknown because the analyst can rarely afford to measure all members of a population, and so a random sample is drawn.
Post-hoc theorizing: Post hoc theorizing is likely to occur when the analyst attempts to explain analysis results after-the-fact. In this second-rate approach to scientific discovery, the analyst develops hypotheses to explain the data, instead of the converse (collecting data to nullify the hypotheses). The number of post-hoc theories that can be developed to ‘fit’ the data is limited only by the imagination of a group of scientists. With an abundance of competing hypothesis, and little forethought as to which hypothesis can be afforded more credence, there is little in the way of statistical justification to prefer one hypothesis to another. More importantly, there is little evidence to eliminate the prospect of illusory correlation.
Power: In general, the power of a statistical test of some hypothesis is the probability that it rejects the alternative hypothesis when the alternative is false. The power is greatest when the probability of a Type II error is least. Power is 1 - b, whereas level of confidence is 1 - a.
Precision: The degree of agreement within a given set of observations.
Prediction interval: A prediction interval is a calculated range of values known to contain some future observation over the average of repeated trials with specific certainty (probability). The correct interpretation of a prediction interval is as follows: If the analyst were to repeatedly draw samples at the same levels of the independent variables and compute the test statistic (mean, regression slope, etc.), then a future observation will lie in the (1-a)% prediction interval a times out of 100. The prediction interval differs from the confidence interval in that the confidence interval provides certainty bounds around a mean, whereas the prediction interval provides certainty bounds around an observation.
Precision: The precision or efficiency of an estimator is its tendency to have its values cluster closely around the mean of its sampling distribution. Precise estimators are preferred to less precise estimators.
Productivity: Unit output per unit of resource input (see also efficiency).
R
Random Error: A deviation of an observed from a true value which occurs as though chosen at random from a probability distribution of such errors.
Randomization: Randomization is used in the design of experiments. When certain factors cannot be controlled, and omitted variable bias has potential to occur, randomization is used to randomly assign subjects to treatment and control groups, such that any systematic omitted variable bias will be distributed evenly among the two groups. Randomization should not be confused with random sampling, which serves to provide a representative sample.
Random sampling: A sample strategy whereby population members have equal probability of being recruited into the sample. Often called simple random sampling, it provides the greatest assurance that the sample is representative of the population of interest.
Random selection: Synonymous with random sampling, a sample selected from a finite population is said to be random if every possible sample has equal probability of selection. This applies to sampling without replacement. A random sample with replacement is still considered random as long as the population is sufficiently large such that the replaced experimental unit has small probability of being recruited into the sample again.
Random variable: A variable whose exact value is not known prior to measurement. Typically, independent variables in experiments are not random variables because their values are assigned or controlled by the analyst. For instance, fertilizer A is applied in exacting quantities to the plant under study, thus amount of fertilizer A is a known constant. In observational studies, in contrast, independent variables are often random variables because the analyst does not control them. For instance, in a study of the effect of acid rain on habitation in the northeast, the analyst cannot control the concentration of pollutants in the rain, and so concentration of contaminant X is a random variable.
Range: The largest minus the smallest of a set of variate values.
Ratio scale: A variable measured on a ratio scale has order, possesses even intervals between levels of the variable, and has an absolute zero. An example of a ratio scale variable is height, where levels of response include 0.000 and 2000 inches. The ratio scale variable provides the statistician with the greatest amount of information relative to other scales of measurement. See also nominal, ordinal, and interval scales of measurement.
Raw data: Data that has not been subjected to any sort of mathematical manipulation or statistical treatment such as grouping, coding, censoring, or transformation.
Regression: A statistical method for investigating the inter-dependence of variables.
Repeatability: Degree of agreement between successive runs of an experiment.
Replication: The execution of an experiment or survey more than once so as to increase the precision and to obtain a closer estimation of the sampling error
Representative Sample: A sample which is representative of a population (it is a moot point whether the sample is chosen at random or selected to be ‘typical’ of certain characteristics; therefore, it is better to use the term for samples which turn out to be representative, however chosen, rather than apply it to a sample chosen with the object of being representative)
Reproducibility: An experiment or survey is said to be reproducible if, on repetition or replication under similar conditions, it gives the same results
Research: Research is a systematic search for facts or information. What separates scientific research from other means for making statements about the universe, society, and the environment is that scientific research is rigorous. It is constantly reviewed by professional colleagues; and it relies on consensus building based on repeated similar results. One of the foundations of research is the scientific method, which relies heavily on statistical methods. Often to the dismay of the general public, the use of statistics and the scientific method cannot prove that a theory, relationship, or hypothesis is true. On the contrary, the scientific method can be used to prove that a theory, relationship, or hypothesis is false. Through consensus building and peer review of scientific work, theories, hypotheses, and relationships can be shown to be highly likely, but there always exists a shred of uncertainty that puts the results at risk of being incorrect, and there may always be an alternative explanation of the phenomenon that better explains the phenomenon scientists are trying to explain.
Residual: A residual is defined as the difference between the observed value and the fitted value in a statistical model. Residual is synonymous with error, disturbance, and statistical noise.
Residual method: In time series analysis, a classical method of estimating cyclical components by first eliminating the trend, seasonal variations, and irregular variations, thus leaving the cyclical relatives as residuals.
Robustness: A method of statistical inference is said to be robust if it remains relatively unaffected when all of its underlying assumptions are not met.
S
Sample: A part or subset of a population, which is obtained through a recruitment or selection process, usually with the objective of understanding better the parent population. Statistics are computed on sample data to make formal statements about the population of interest. If the sample is not representative of the population, then statements made based on sample statistics will be incorrect to some degree.
Sample Size: The number of sampling units which are to be included in the sample
Sampling Error: That part of the difference between a population value and an estimate thereof, derived from a random sample, which is due to the fact that only a sample of values is observed
Scatter Diagram: Graph showing two corresponding scores for an individual as a point; the result is a swarm of points
Science: Science is the accumulation of knowledge acquired by careful observation, by deduction of the laws that govern changes and conditions, and by testing these deductions by experiment. The scientific method is the cornerstone of science, and is the primary mechanism by which scientists make statements about the universe and phenomenon within it.
Scientific Method: The theoretical and empirical processes of discovery and demonstration considered characteristic and necessary for scientific investigation, generally involving observation, formulation of a hypothesis, experimentation to provide support for the truth or falseness of the hypothesis, and a conclusion that validates or modifies the original hypothesis. The scientific method cannot be used to prove that a hypothesis is true, but can be used to disprove a hypothesis; however, it can be used to mount substantial evidence in support of a particular hypothesis, theory, or relationship.
Seasonal cycle length: The length of the characteristic recurrent pattern in seasonal time series, given in terms of number of discrete observation intervals.
Seasonal differencing: Creating a transformed series by subtracting observations that are separated in time by one seasonal cycle.
Seasonality: The time series characteristic defined by a recurrent pattern of constant length in terms of discrete observation intervals.
Self-selection: Self-selection is a problem that plagues survey research. Self-selection is a term used to describe what happens when survey respondents are allowed to deny participation in a survey. The belief is that respondents who are opposed or who are apathetic about the objectives of the survey will refuse to participate, and their removal from the sample will bias the results of the survey. Self-selection can also occur because respondents who are either strongly opposed or strongly supportive of a survey’s objectives respond to the survey. A classic example is television news polls that solicit call in responses from listeners—the results from which are practically useless for learning how the population at large feels about an issue.
Significance: An effect is significant if the value of the statistic used to test it lies outside acceptable limits i.e. if the hypothesis that the effect is not present is rejected
Skewness: Skewness is the lack of symmetry in a probability distribution. In a skewed distribution the mean and median are not coincident.
Smoothing: The process of removing fluctuations in an ordered series so that the result will be ‘smooth’ in the sense that the first differences are regular and higher order differences are small. Although smoothing can be carried out by freehand methods, it is usual to make use of moving averages or the fitting of curves by least squares procedures. The philosophical grounds for smoothing stem from the notion that measurements are made with error, such that artificial “bumps” are observed in the data, whereas the data really should represent a smooth or continuous process. When these “lumpy” data are smoothed appropriately, the data are thought to better reflect the true process that generated the data. An example is the speed-time trace of a vehicle, where speed is measured in integer miles per hour. Accelerations of the vehicle computed from differences in successive speeds will be over-estimated due to the lumpy nature of measuring speed. Thus an appropriate smoothing process on the speed data will result in data that more closely resembles the underlying data generating process. Of course the technical difficulty with smoothing lies in selecting the appropriate smoothing process, since the real data are never typically observed.
Standard deviation: The sample standard deviation si is the square root of the sample variance and is given by the formula:
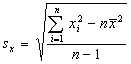
where n is the sample size and xave is the sample mean. The sample standard deviation shown here is a biased estimator, even though the sample variance is unbiased, and the bias becomes larger as the sample size gets smaller.
Standard Error: The positive square root of the variance of the sampling distribution of a statistic
Standard Error of the Mean: Standard deviation of the means of several samples drawn at random from a large population
Standard Error of Estimate: The standard deviation of the observed values about a regression line
Standard normal transformation: Fortunately, the analyst can transform any normal distributed variable into a standard normal distributed variable by making use of a simple transformation. Given a normally distributed variable X, we define Z such that:
![]()
The new variable Z is normally distributed with m=0 and s=1, and is a standard normal variable.
Standard Scores: Scores expressed in terms of standard deviations away from the mean
Statistic: A summary value calculated from a sample of observations
Statistics: The branch of mathematics that deals with all aspects of the science of decision-making and analysis of data in the face of uncertainty.
![]()
Statistical independence: In probability theory, two events are said to be statistically independent if, and only if, the probability that they will both occur equals the product of the probabilities that each one, individually will occur i.e. one event does not depend on another for its occurrence or non-occurrence. In statistical notation, statistical independence is given by:
where P(A Ç B) is the probability that both event A and B occur.
Statistical inference: Also called inductive statistics, statistical inference is a form of reasoning from sample data to population parameters; that is, any generalization, prediction, estimate, or decision based on a sample and made about the population. There are two schools of thought in statistical inference, classical or frequentist statistics for which R. A. Fisher is considered to be the founding father, and Bayesian inference, discovered by a man bearing the same name.
Statistical methods: Statistical methods are similar to a glass lens through which the analyst inspects phenomenon of interest. The underlying mechanisms present in the population represents reality, the sample represents a blurry snapshot of the population, and statistical methods represent a means of quantifying various aspects of the sample.
Stochastic: The adjective ‘stochastic’ implies that a process or data generating mechanism involves a random component or components. A statistical model consists of stochastic and deterministic components.
Stratification: The division of a population into parts, known as strata
Stratified random sampling: A method of sampling from a population whereby the population is divided into parts, known as strata, especially for the purpose of drawing a sample, and then assigned proportions of the sample are then sampled from each stratum. The process of stratification is undertaken in order to reduce the variability of stratification statistics. In other words, strata are generally selected such that inter-strata variability is maximized, and intra-strata variability is small. When stratified sampling is performed as desired, estimates of strata statistics are more precise than the same estimates computed on a simple random sample.
Systematic Error: An error, which is in some sense biased, having a distribution with a mean that is not zero (as opposed to a random error)
T
Technology: The science of technical processes is a wide, though related, body of knowledge. Technology embraces the chemical, mechanical, electrical, and physical sciences as they are applied to society, the environment, and otherwise human endeavors.
Technology Transfer: The dissemination of knowledge leading to the successful implementation of the results of research and development. Technology transfer outputs from a research project, such as prototypes, software, devices, specifications designs, processes, or practices, etc. are either expendable or often have only temporary and limited utility.
Time Series: A time series is a set of ordered observations on a quantitative characteristic of an individual or collective phenomenon taken at different points of time. Although it is not a requirement, it is common for these points to be equidistant in time.
Transformation: A transformation is the change in the scale of a variable. Transformations are performed to simplify calculations, to meet specific statistical modeling assumptions, to linearize an otherwise non-linear relation with another variable, to impose practical limitations on a variable, and to change the characteristic shape of a probability distributions of the variable in its original scale.
Transportation: The act and/or means for moving people and goods.
Truncated distribution: A truncated statistical distribution occurs when a response above or below a certain threshold value is discarded. For instance, assume that certain instrumentation that can only read measurements within a certain range—data obtained from this instrument may result in a truncated distribution, as measurements outside the range are discarded. If measurements were recorded at the extreme range of the measurement device, then the distribution would be censored.
t Distribution: Distribution of values with particular degrees of freedom of difference between sample and population mean divided by the standard error of mean
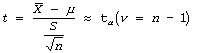
t-statistic: When a sample is used to calculate s2, an estimate of the population variance s2, and the parent population is normally distributed, the sampling distribution of the test statistic t is approximately t distributed is given by:
where n is the sample size.
Two-tailed Test: A test of significance in which both directions are, a priori, equally likely
Type I error: If, as the result of a test statistic computed on sample data, a statistical hypothesis is rejected when it should be accepted, i.e. when it is true, then a type I error has been made. Alpha, or level of significance, is pre selected by the analyst to determine the type I error rate. The level of confidence of a particular test is given by 1 – alpha.
Type II error: If, as the result of a test statistic computed on sample data, a statistical hypothesis is accepted when it is false, i.e. when it should have been rejected, then a type II error has been made. Beta is pre selected by the analyst to determine the type II error rate. The Power of a particular test is given by 1 – beta.
U
Unbiased Estimator: An estimator whose expected value (namely the mean of the sampling distribution) equals the parameter it is supposed to estimate. In general unbiased estimators are preferred to biased estimators of population parameters. There are rare cases, however, when biased estimators are preferred because they are much more efficient than alternative estimators.
Uniform distribution: Uniform distributions are appropriate for cases when the probability of obtaining an outcome within a range of outcomes is constant. An example is the probability of observing a crash at a specific location between two consecutive post miles on a homogenous section of freeway. The probability density function for the continuous uniform distribution is given by:
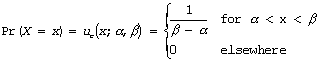
where, x is the value of random variable X, a is the lower most value of the interval for x, and b is the upper most value of the interval for x.
Universe: Universe is synonymous with population and is found primarily in older statistical textbooks. Most newer textbooks and statistical literature uses population to define the experimental units of primary interest.
V
Validity: Degree to which some procedure is founded on logic (internal or formal validity) or corresponds to nature (external or empirical validity)
Validation: Validation is a term used to describe the important activity of validating a statistical model. The only way to validate the generalizability or transferability of an estimated model is to make forecasts with a model and compare them to data that were not used to estimate the model. This exercise is called external validation. The importance of this step of model building cannot be overstated, but it remains perhaps the least practiced step of model building, because it is expensive and time consuming, and because some modelers and practitioners confuse goodness of fit statistics computed on the sample data with the same computed on validation data.
Variable: A quantity that may take any one of a specified set of values
Variability: Variability is a statistical term used to describe and quantify the spread or dispersion of data around its center, usually the mean. Knowledge of data variability is essential for conducting statistical tests and for fully understanding data. Thus, it is often desirable to obtain measures of both central tendency and spread. In fact, it may be misleading to consider only measures of central tendency when describing data.
Variance: Square of standard deviation
Variate: A quantity that may take any of the values of a specified set with a specified relative frequency or probability, also known as a random variable
W
Weight: A numerical coefficient attached to an observation, frequently by multiplication, in order that it shall assume a desired degree of importance in a function of all the observations of the set
Weighted Average: An average of quantities to which have been attached a series of weights in order to make allowance for their relative importance
White noise: For time series analysis, white noise is defined as a series whose elements are uncorrelated and normally distributed with mean zero and constant variance. The residuals from properly specified and estimated time series models should be white noise.
Z
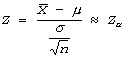
Z-statistic: If xave is calculated on a sample selected from a distribution with mean m and known finite variance s2, then the sampling distribution of the test statistic Z is approximately standard normal distributed, regardless of the characteristics of the parent distribution (i.e. normal, Poisson, binomial, etc.). Thus, a random variable Z computed as follows is approximately standard normal (mean=0, variance=1) distributed: